一,前缀和:
前缀和就是前n项和,通过提前计算前n项和,根据前n项和的性质来计算出某段区间的和
前缀和的定义:
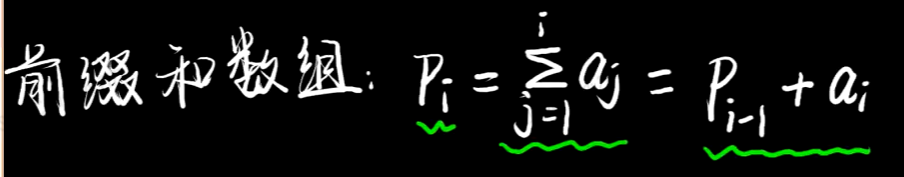
前缀和的性质:
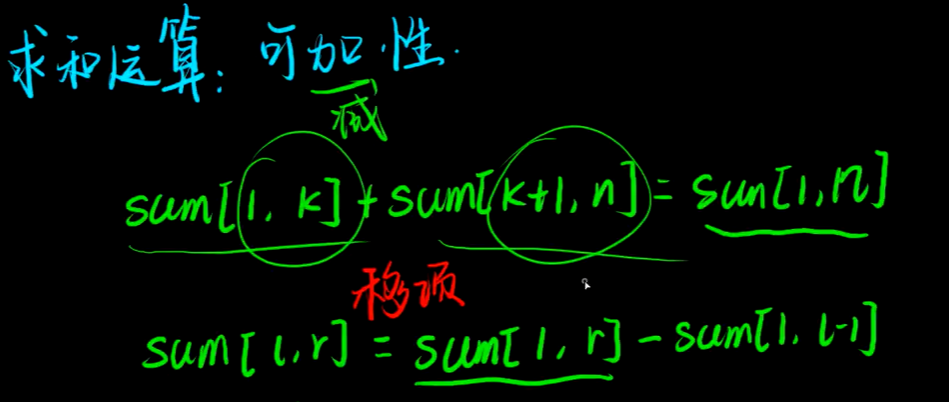
前缀和的求解表达式

https://www.starrycoding.com/problem/7
// Problem: ${前缀和}
// Contest: ${json.group}
// URL: ${https://www.starrycoding.com/problem/7}
// Memory Limit: ${128} MB
// Time Limit: ${500} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
void solve() {
int T;
cin >> T;
while (T--) {
int n, q;
cin >> n >> q;
vector<int> n_i_sum(n + 1, 0);
for (int i = 1; i <= n; i++) {
int n_i_num;
cin >> n_i_num;
n_i_sum[i] = n_i_sum[i - 1] + n_i_num;
}
while (q--) {
int l, r;
cin >> l >> r;
cout << n_i_sum[r] - n_i_sum[l - 1] << endl;
}
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}二,差分数组:
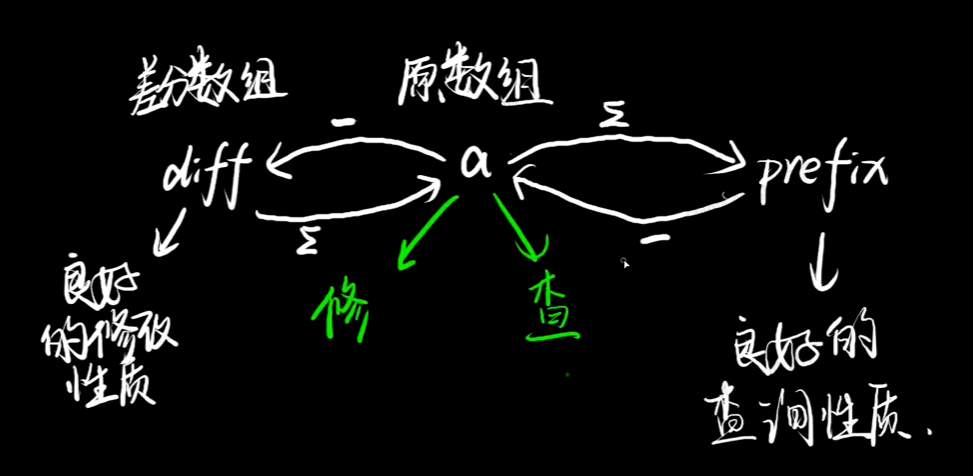
方法一(DP):
差分数组的定义与功能
可以将式子变换为ai=di+ai-1(在前缀和思想的基础上,可以将ai视为dj的前i项和),主要用于解决对a_i范围修改的问题
即转化为这种格式

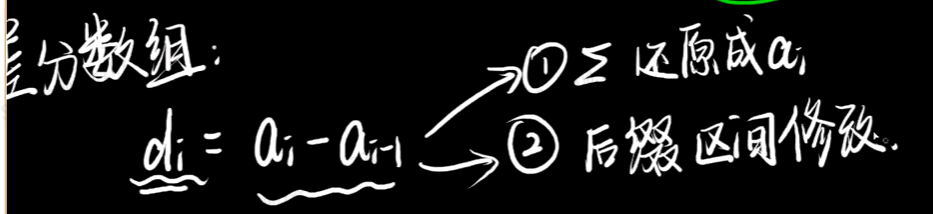
功能一,对di进行前缀和可以还原成ai
同时,我们得知ai为dj的前i项和
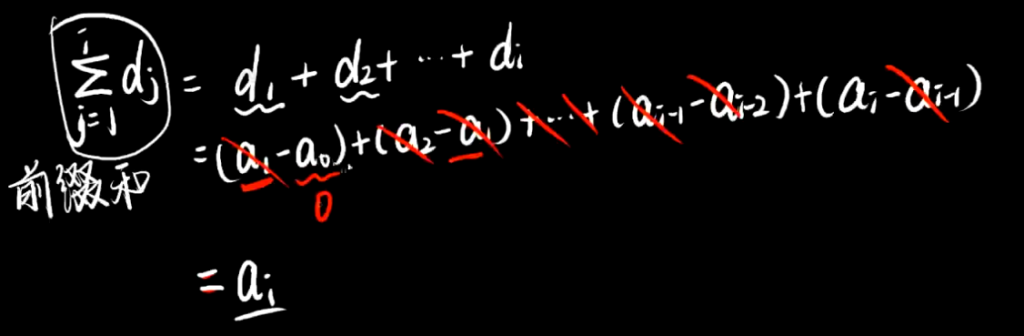
功能二,后缀区间修改
通过修改di可以改变ai的值,从而可以改变某一段区间的值
如图:
对d_2进行+x,可以使,a_2,a_3,a_4…均+x,同时对d_4-x,可以使a_4及其之后的a_…均-x,这样便实现了对a_2,a_3+x,而其他a_..不变.
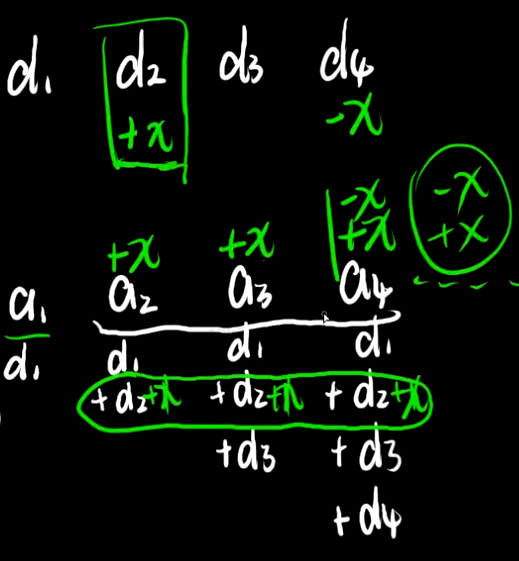
解题步骤:

https://www.starrycoding.com/problem/8
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
void solve() {
int n, p, q;
cin >> n >> p >> q;
vector<int> a_i(n + 9, 0);
vector<int> a_i_diff(n + 9, 0);
vector<int> a_i_sum(n + 9, 0);
for (int i = 1; i <= n; i++) {
cin >> a_i[i];
}
for (int i = 1; i <= n; i++) {
a_i_diff[i] = a_i[i] - a_i[i - 1];
}
while (p--) {
int l_1, r_1, x;
cin >> l_1 >> r_1 >> x;
a_i_diff[l_1] += x;
a_i_diff[r_1 + 1] -= x;
}
for (int i = 1; i <= n; i++) {
a_i[i] = a_i[i - 1] + a_i_diff[i];
}
for (int i = 1; i <= n; i++) {
a_i_sum[i] = a_i_sum[i - 1] + a_i[i];
}
while (q--) {
int l, r;
cin >> l >> r;
cout << a_i_sum[r] - a_i_sum[l - 1] << endl;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}方法二(模拟):
和下文的二维差分用的思路一致,均为模拟,即,先产生修改点数组,再使用一个数组来对修改点数组模拟,最后将模拟数组与原数组相加,即得到解
修改点数组:

模拟修改点数组:

与原数组相加:

原数组前缀和:

前缀和相减即得解
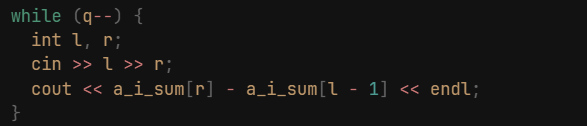
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
void solve() {
int n, p, q;
cin >> n >> p >> q;
vector<int> a_i(n + 9, 0);
vector<int> a_i_q(n + 9, 0);
vector<int> a_i_next(n + 9, 0);
vector<int> a_i_sum(n + 9, 0);
for (int i = 1; i <= n; i++) {
cin >> a_i[i];
}
while (p--) {
int l_1, r_1, x;
cin >> l_1 >> r_1 >> x;
a_i_q[l_1] += x;
a_i_q[r_1 + 1] -= x;
}
for (int i = 1; i <= n; i++) {
a_i_next[i] = a_i_next[i - 1] + a_i_q[i];
}
for (int i = 1; i <= n; i++) {
a_i[i] += a_i_next[i];
}
for (int i = 1; i <= n; i++) {
a_i_sum[i] = a_i_sum[i - 1] + a_i[i];
}
while (q--) {
int l, r;
cin >> l >> r;
cout << a_i_sum[r] - a_i_sum[l - 1] << endl;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}二维前缀和:
和一维前缀和原理一样,都是求某区间的和,只是涉及更多方向,画图想想就明白了
定义:

具体化:
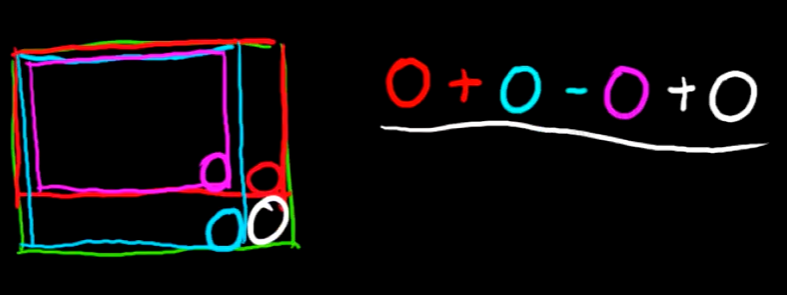
求解表达式:
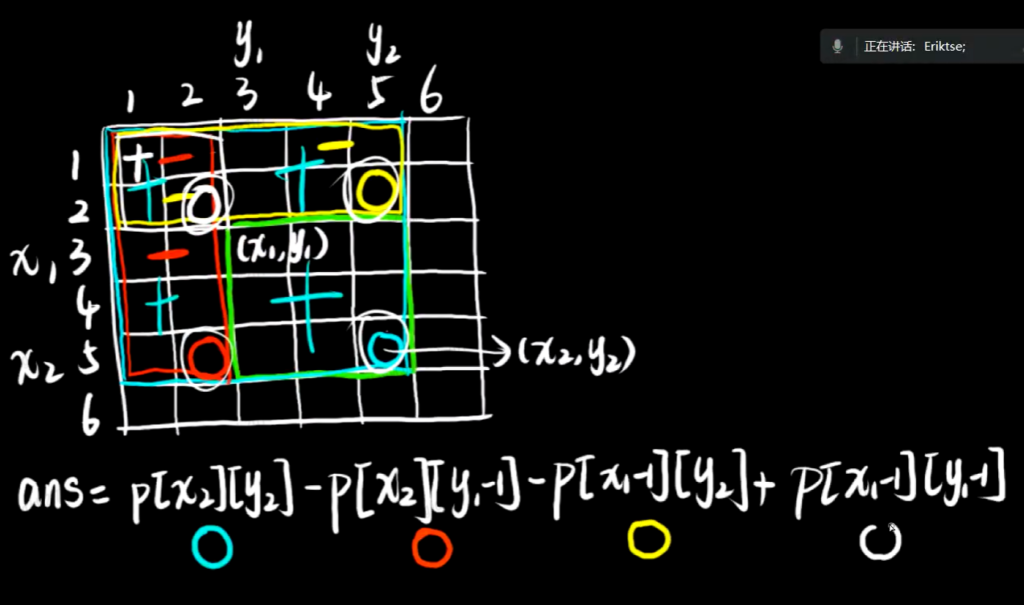
https://www.starrycoding.com/problem/15
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
void solve() {
int n, m, q;
cin >> n >> m >> q;
vector<vector<int>> x_y_sum(n + 1e1, vector<int>(m + 1e1, 0));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int x_y_num;
cin >> x_y_num;
x_y_sum[i][j] = x_y_sum[i][j - 1] + x_y_sum[i - 1][j] -
x_y_sum[i - 1][j - 1] + x_y_num;
}
}
while (q--) {
int x_1, y_1, x_2, y_2;
cin >> x_1 >> y_1 >> x_2 >> y_2;
cout << x_y_sum[x_2][y_2] - x_y_sum[x_1 - 1][y_2] - x_y_sum[x_2][y_1 - 1] +
x_y_sum[x_1 - 1][y_1 - 1]
<< endl;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}二维差分(模拟法):
与差分相同的原理,但是提供了新的思路,因为二维差分的表达式难表达,故先产生修改点数组,再使用一个数组来对修改点数组模拟,最后将模拟数组与原数组相加,即得到解
同样的,一维数组也可以使用这种思路,即一共使用四个数组,比正常多一个
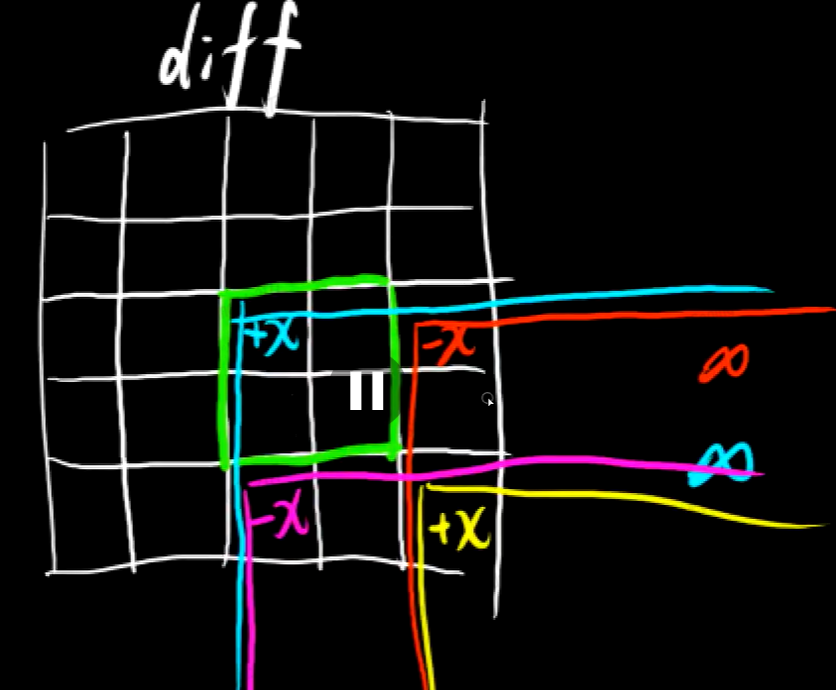
关键步骤,用来存储修改,其中的修改点值得思考:
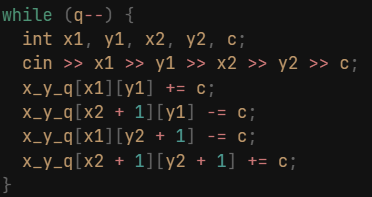
对修改点数组进行模拟:
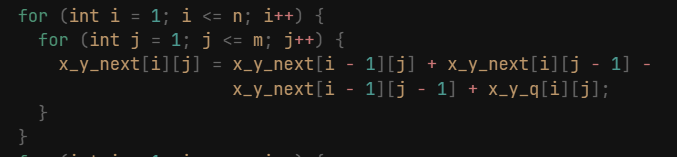
将模拟数组与原数组相加:
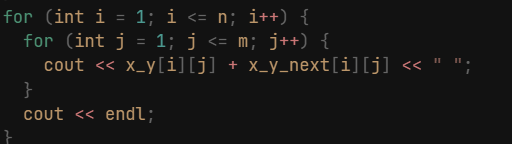
前缀和数组的具体化,但如何实现呢?
https://www.starrycoding.com/problem/50
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
void solve() {
int n, m, q;
cin >> n >> m >> q;
vector<vector<int>> x_y(n + 1e1, vector<int>(m + 1e1, 0));
vector<vector<int>> x_y_q(n + 1e1, vector<int>(m + 1e1, 0));
vector<vector<int>> x_y_next(n + 1e1, vector<int>(m + 1e1, 0));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> x_y[i][j];
}
}
while (q--) {
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
x_y_q[x1][y1] += c;
x_y_q[x2 + 1][y1] -= c;
x_y_q[x1][y2 + 1] -= c;
x_y_q[x2 + 1][y2 + 1] += c;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
x_y_next[i][j] = x_y_next[i - 1][j] + x_y_next[i][j - 1] -
x_y_next[i - 1][j - 1] + x_y_q[i][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << x_y[i][j] + x_y_next[i][j] << " ";
}
cout << endl;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}https://www.starrycoding.com/problem/35
前缀和做法:(DP)
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
void solve() {
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
vector<int> type_animal(n + 10, 0);
vector<int> weight_animal(n + 10, 0);
vector<int> prefix(n + 10, 0);
for (int i = 1; i <= n; i++) {
cin >> type_animal[i];
}
for (int i = 1; i <= n; i++) {
cin >> weight_animal[i];
}
int ess = 0;
for (int i = 1; i <= n; i++) {
ess += type_animal[i] * weight_animal[i];
}
int mi = 0, fix = 0;
for (int i = 1; i <= n; i++) {
prefix[i] = prefix[i - 1] + (type_animal[i] ? -1 : 1) * weight_animal[i];//2,-3,3,8
fix = max(fix, prefix[i] - mi);//2,2,6,11
mi = min(mi, prefix[i]);//0,-3,-3,-3
}
cout << ess + fix << endl;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}贪心做法:(贪心)
好理解一点
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
void solve() {
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
vector<int> type_animal(n + 10, 0);
vector<int> weight_animal(n + 10, 0);
vector<int> prefix(n + 10, 0);
for (int i = 1; i <= n; i++) {
cin >> type_animal[i];
}
for (int i = 1; i <= n; i++) {
cin >> weight_animal[i];
}
int ess = 0;
//不变:
for (int i = 1; i <= n; i++) {
ess += type_animal[i] * weight_animal[i]; //鸭鸭最初的重量
}
//变化:
int mx = 0, fix = 0;
for (int i = 1; i <= n; i++) {
mx = max(0ll,
mx + (type_animal[i] ? -1 : 1) * weight_animal[i]); //子段最值
fix = max(fix, mx); //全局最值(根据子段最值求出全局最值)
}
cout << ess + fix << endl;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}