题目:leetcode704.二分查找
https://leetcode.cn/problems/binary-search/description/
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入:nums= [-1,0,3,5,9,12],target= 9 输出: 4 解释: 9 出现在nums中并且下标为 4
示例 2:
输入:nums= [-1,0,3,5,9,12],target= 2 输出: -1 解释: 2 不存在nums中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
这种题目的前提是数组为有序数组(可不可以自己排序?),同时题目还要求数组无重复元素,因为一旦由重复元素,那么使用二分法返回的元素下标可能不是唯一的,这些都是使用二分的前提条件,当看到题目描述满足以上条件时,就要想一想可不可以用二分法了
二分法虽然说逻辑比较简单,但是涉及很多边界条件,很容易写错例如:时while(left<right)还是while(left<=right),到底是right=middle还是right=middle-1
经常写错的原因是不清楚区间的定义,区间的定义就是”不变量”.要在二分查找的过程中保持”不变量”——在while循环中,每一次边界的处理都根据区间的定义来操作,这就是”循环不变量”规则
二分法中间区的定义一般有两种,一种是左闭右闭即[left,right],另一种是左闭右开即[left,right),下面基于这两种区间的定义分别讲解两种不同的二分法写法
写法一:[left,right]
- 定义target在一个左闭右闭的区间,也就是[left,right]区间是有意义的,所以while(left<=right)中要使用<=
- 如果nums[middle]大于tagret,则更新搜索范围右下标right为middle-1.因为当前这个nums[middle]一定不是target,所以接下来要查找的左区间结束下标位置是middle-1
- 代码推写是循序渐进的,首先知道while循环中左闭右闭,于是判断middle是否会被选上,因为两边均为闭,所以知道会被选上,故为middle-1/middle+1,以避免middle不会被选上
例:
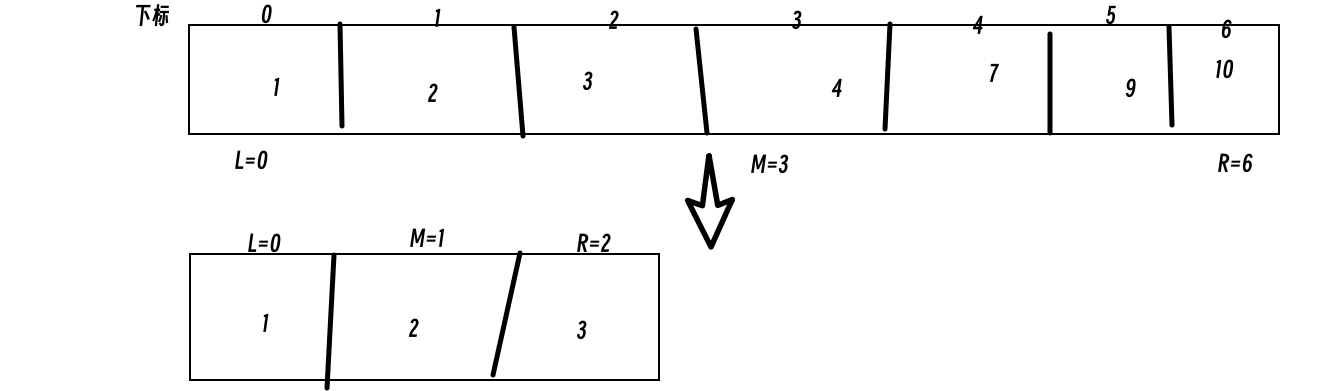
代码:
class solution
{
public:
int search(vector<int> &nums, int target)
{
int left = 0;
// 由于是闭区间,所以right = nums.size() - 1
int right = nums.size() - 1;
//当left == right时,区间[left, right]仍然有效
while (left <= right)
{
// 防止溢出,等同于(left + right) / 2
int middle = left + ((right - left) / 2);
if (nums[middle] > target)
{
right = middle - 1;// target在左区间
} else if (nums[middle] < target)
{
left = middle + 1;// target在右区间
} else
{
return middle;//找到目标值
}
}
return -1;// 未找到目标值
}
};
写法二:[left,right)
- while(left<right),这里使用”<“是因为left与right相同时时没有意义的
- 如果nums[middle]大于target,则更新搜索范围右下标right为middle.因为当前nums[middle]不等于target,那么继续去左区间查找,而寻找的区间是左闭右开,所以right更新为middle,即在下一个查询区间不会比较nums[middle]
- 首先知道while循环时左闭右开,于是判断middle是否会被选上,当middle小于target时,使left更改,因为left为闭,所以left=midlle+!,当middle大于target,使right更改,因为right为开,所以middle不会被选上,所以right=middle
例:
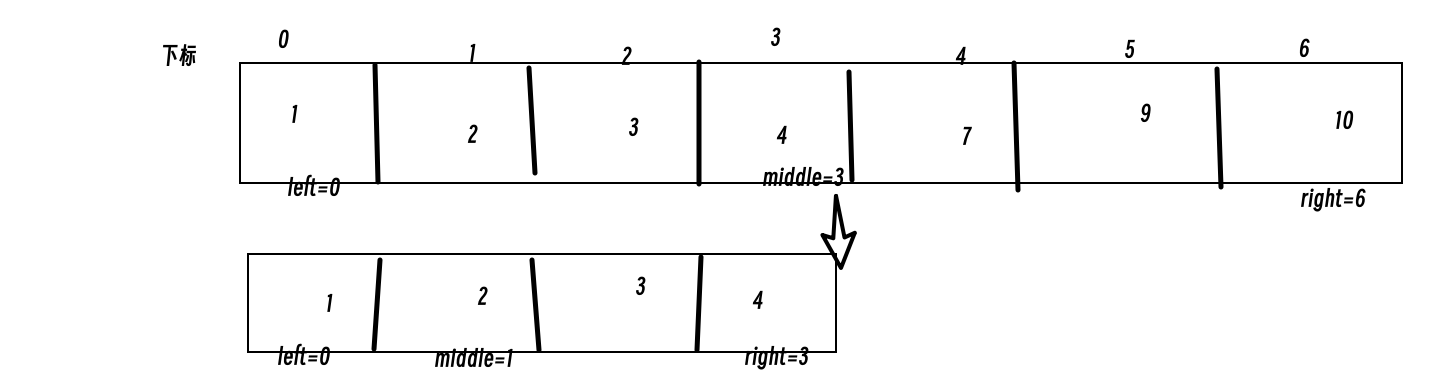
代码:
class solution
{
public:
int search(vector<int> &nums, int target)
{
int left = 0;
// 由于是开区间,所以right = nums.size()
int right = nums.size();
//当left == right时,区间[left, right)仍然有效
while (left < right)
{
// 防止溢出,等同于(left + right) / 2
int middle = left + ((right - left) / 2);
if (nums[middle] > target)
{
right = middle;// target在左区间
} else if (nums[middle] < target)
{
left = middle + 1;// target在右区间
} else
{
return middle;//找到目标值
}
}
return -1;// 未找到目标值
}
};