离散化:
与其叫离散化,我更喜欢叫它为聚集化,我认为其实现原理为:
将离散的数据聚集(离散表),排序去重形成聚集表,生成对应存值表,两个表的联系为相同下标的指向数据相同,聚集表存储的是数据,存值表存储的数据的值,通过这种方式,可以有效聚集离散的数据使其更加紧凑,两个数组的下标联系用一个函数链接,在聚集表中使用此函数找到对应数据的下标,在存值表中用此下标访问此数据的值
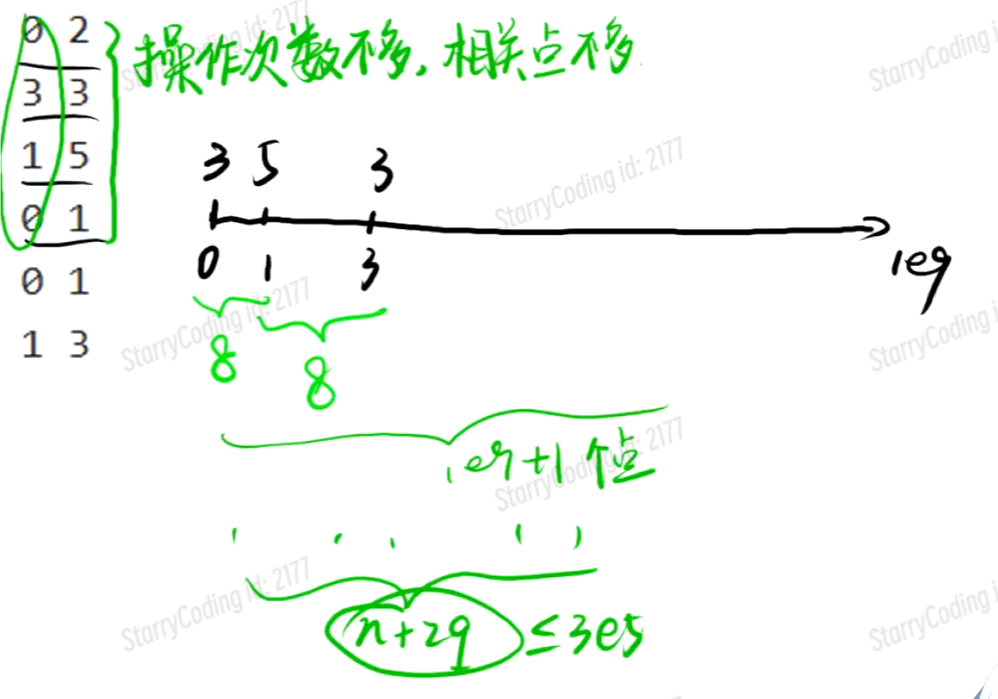



https://www.starrycoding.com/problem/63
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N = 3e5 + 9;
vector<int> vec;
int res[N];
struct Q {
int a, b;
} add[N], que[N];//用一个自定义类型实现输入与输出序对
auto find_x(int x) {
return lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;
}//查找下标函数
void solve() {
int n, q;
cin >> n >> q;
for (int i = 1; i <= n; i++) {
int x, w;
cin >> x >> w;
add[i] = {x, w};//初始化输入数据
vec.push_back(x);//将x存入离散表
}
for (int i = 1; i <= q; i++) {
int l, r;
cin >> l >> r;
vec.push_back(l);//将l存入离散表
vec.push_back(r);//将r存入离散表
que[i] = {l, r};//初始化输出数据
}
sort(vec.begin(), vec.end());
vec.erase(unique(vec.begin(), vec.end()), vec.end());//排序去重以形成聚集表
for (int i = 1; i <= n; i++) {
res[find_x(add[i].a)] += add[i].b;//在聚集表中查找输入数据以访问存值表
}
for (unsigned int i = 1; i <= vec.size(); i++) {
res[i] += res[i - 1];//对存值表前缀和
}
for (int i = 1; i <= q; i++) {
cout << res[find_x(que[i].b)] - res[find_x(que[i].a) - 1] << endl;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int _ = 1;
while (_--) solve();
return 0;
}树状数组:(单点)
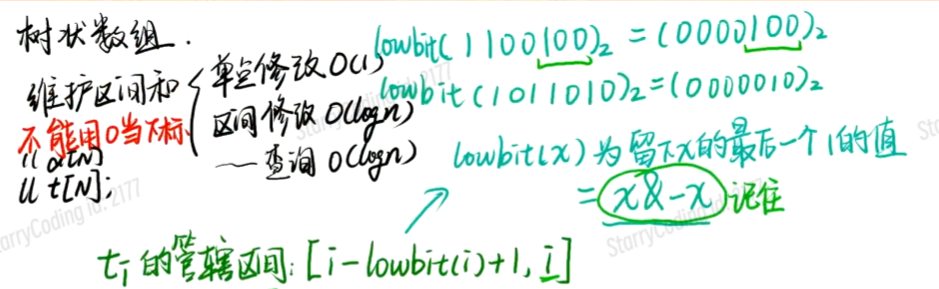
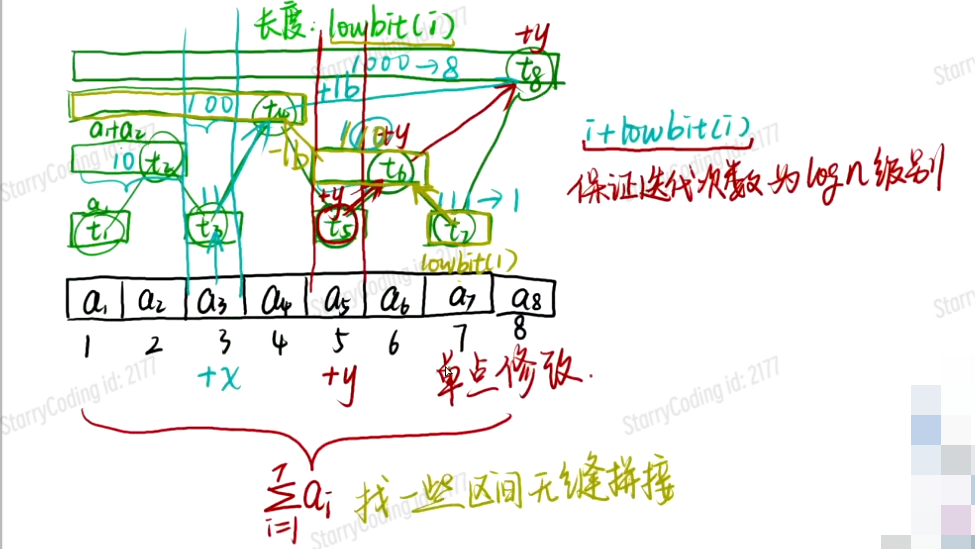
基本思路:
创建一个新数组t[N],用t来存储原数组的子缀和,且根据二进制的lowbit来表示所求范围
lowbit性质:可以访问与其有相同范围的子段,可以获取与其位置相连的子段
https://www.starrycoding.com/problem/40
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N = 2e5 + 9;
int a[N], m[N];
int n, q;
int lowbit(int x) { return x & -x; }//lowbit的表达方式,获取最低位1的剩余部分
void upthis(int k, int v) {
for (int i = k; i <= n; i += lowbit(i)) {//对m数组进行更改操作,运用lowbit的性质
m[i] += v;
}
}
int outthis(int t) {
int res = 0;
for (int i = t; i >= 1; i -= lowbit(i)) {//对m数组求前缀和,运用lowbit的性质
res += m[i];
}
return res;
}
void solve() {
cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) upthis(i, a[i]);
for (int i = 1; i <= q; i++) {
int fuck;
cin >> fuck;
if (fuck == 1) {
int k, v;
cin >> k >> v;
upthis(k, v);
} else {
int l, r;
cin >> l >> r;
cout << outthis(r) - outthis(l - 1) << endl;//前缀和求区间
}
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}树状数组:(区间)//晕
使用差分:

https://www.starrycoding.com/problem/41
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N = 2e5 + 9;
int a[N], m[N], tid[N];
int n, q;
int lowbit(int x) { return x & -x; }
void upthis(int k, int v) {
for (int i = k; i <= n; i += lowbit(i)) {
m[i] += v;
tid[i] += k * v;
}
}
int outthis(int t) {
int res = 0;
for (int i = t; i >= 1; i -= lowbit(i)) {
res += (t + 1) * m[i] - tid[i];
}
return res;
}
void solve() {
cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
upthis(i, a[i]);
upthis(i + 1, -a[i]);
}
for (int i = 1; i <= q; i++) {
int fuck;
cin >> fuck;
if (fuck == 1) {
int k, r, v;
cin >> k >> r >> v;
upthis(k, v);
upthis(r + 1, -v);
} else {
int l, r;
cin >> l >> r;
cout << outthis(r) - outthis(l - 1) << endl;
}
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}https://www.starrycoding.com/problem/31
结合离散化和树状数组:(有一丢丢难)
// Problem: ${json.name}
// Contest: ${json.group}
// URL: ${json.url}
// Memory Limit: ${json.memoryLimit} MB
// Time Limit: ${json.timeLimit} ms
// More thought is needed
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N = 2e5 + 9;
int a[N], t[N];
vector<int> X;
int lowbit(int x) { return x & -x; }
int bin(int x) { return lower_bound(X.begin(), X.end(), x) - X.begin() + 1; }
void update(int k, int x) {
for (unsigned int i = k; i <= X.size(); i += lowbit(i)) {
t[i] += x;
}
}
int getsum(int k) {
int res = 0;
for (int i = k; i >= 1; i -= lowbit(i)) {
res += t[i];
}
return res;
}
void solve() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
X.push_back(a[i]);
}
sort(X.begin(), X.end());
X.erase(unique(X.begin(), X.end()), X.end());
int ans = 0;
for (int i = 1; i <= n; i++) {
ans += 1ll * getsum(X.size()) - getsum(bin(a[i]));
update(bin(a[i]), 1);
}
cout << ans << endl;
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}