滑动窗口

题目leetcode209.长度最小的子数组

https://leetcode.cn/search/?q=209

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 

子数组[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

进阶：

• 如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

---

所谓滑动窗口,就是不断地调节子数组的起始位置和终止位置,从而得到我们想要的结果.以题目中的情况为例:

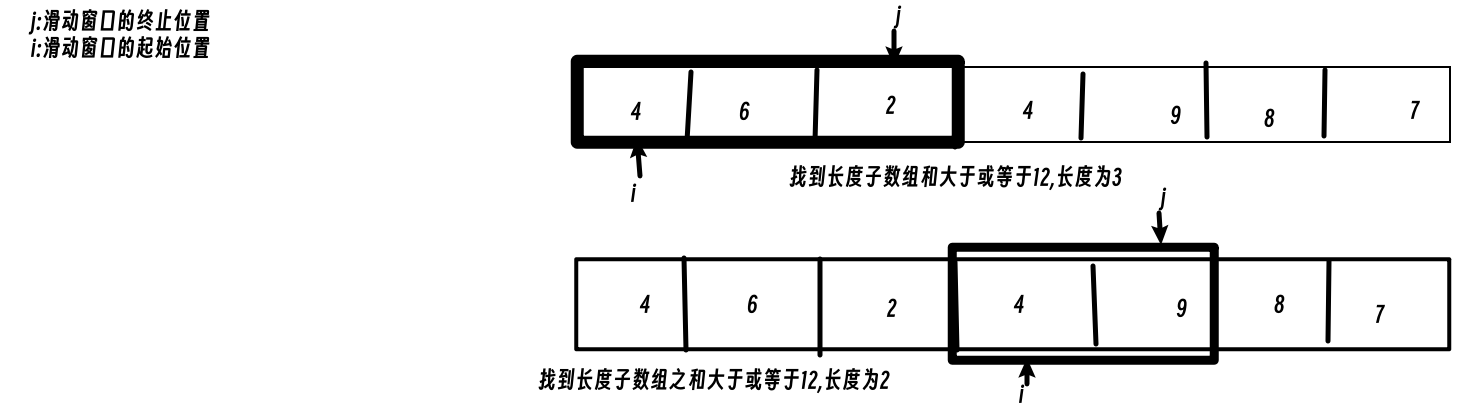
最后找到的[4,9]是满足条件的子数组

滑动窗口可以理解为双指针法的一种,只不过这种解法更像是一个窗口的移动.在本题中实现滑动窗口,主要是确定以下三点:

• 窗口内的元素是什么?
• 如何移动窗口的起始位置?
• 如何移动窗口的终止位置?

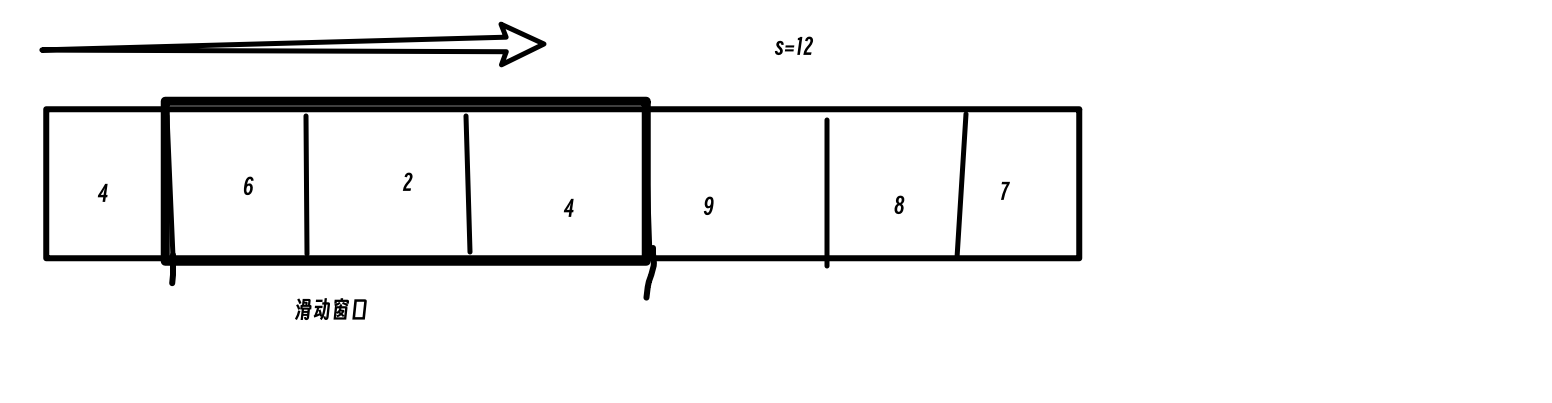
窗口内的元素:保持窗口内数值综合大于或等于s的长度最小的连续子数组

移动窗口的起始位置:如果当前窗口的值大于s,则窗口向前移动(也就是窗口该缩小了)

移动窗口的结束位置:窗口的结束位置就是for循环遍历数组的指针

解题关键在于如何移动窗口的起始位置,如图:

代码:

class Solution
    {
    public:
        int minSubArrayLen(int s, vector<int> &nums)
            {
                int result = INT_MAX;
                int sum = 0;//记录当前滑动窗口的和
                int i = 0;//滑动窗口的起始位置
                int subLength = 0;//滑动窗口的长度
                for (int j = 0; j < nums.size(); j++)
                    {
                        sum += nums[j];
                        //如果当前滑动窗口的和大于等于s，那么就可以开始移动滑动窗口的起始位置
                        while (sum >= s)
                            {
                                subLength = j - i + 1;//计算当前滑动窗口的长度
                                result = min(result, subLength);//更新最小的滑动窗口的长度
                                sum -= nums[i++];//滑动窗口的精髓之处,不断变更i(滑动窗口的起始位置)
                                //如果sum仍大于等于s,则result变小,本题只要求了求最小长度,没有要求具体位置,当sum不满足条件时,则result不变化,即每次while循环结束都能保证当前的长度为最短-1,因为没有要求求和最小,所以只需记录长度即可
                            }
                    }
                //如果result没有被更新过，说明没有找到满足条件的滑动窗口
                return result == INT_MAX ? 0 : result;
            }
    };

时间复杂度:O(n)

空间复杂度:O(1)