空间复杂度

空间复杂度（Cpace Complexity）是对一个算法在运行过程中占用内存大小的度量,记作S(n)=O(f(n)),基于空间复杂度,我们可以预先估计程序运行需要消耗多少内存

空间复杂度的相关问题:

1.空间复杂度考虑程序(可执行文件)的大小吗?

很多人都会混淆程序运行时内存的大小和程序本身的大小.空间复杂度考虑的是程序运行时占用内存的大小,而不是可执行文件的大小

2.空间复杂度可以精确计算出程序运行时占用的内存值吗?

仅仅是估计,很多因素影响运行时占用的内存

O(1)的空间复杂度:

/**
 * ClassName: ${NAME}
 * package: ${PACKAGE_NAME}
 * Description:
 * @Author: innno
 * @Create: 2024/2/27 - 21:54
 * @Version: v1.0
 */
#include <bits/stdc++.h>

using namespace std;

int main()
    {
        ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
        int j = 0,n;cin>>n;
        for(int i = 0; i < n; i++)
        {
            j++;
        }
        return 0;
    }

消耗的内存空间不会随着n的变化而变化,即此算法的空间复杂度为一个常量,表示为O(1)

O(n)的空间复杂度:

/**
 * ClassName: ${NAME}
 * package: ${PACKAGE_NAME}
 * Description:
 * @Author: innno
 * @Create: 2024/2/27 - 21:54
 * @Version: v1.0
 */
#include <bits/stdc++.h>

using namespace std;

int main()
    {
        ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
        int n;cin>>n;
        int *a = new int(n);
        for (int i = 0; i < n; i++)
            {
                a[i] = i;
            }
        free(a);
        return 0;
    }

当消耗空间和输入参数n保持线性增长时,这时的空间复杂度为O(n)

我们定义了一个数组,长度为n,虽然有一个for循环,但没有再分配新的空间,随着n的增大,占用的内存大小呈线性增长,即空间复杂度为O(n)

当递归的时候可能会出现空间复杂度为logn

递归算法的空间复杂度分析:

1.斐波那契的性能分析:

int fibonacci(int i)
    {
        if (i <= 0)return 0;
        if (i == 1)return 1;
        return fibonacci(i - 1) + fibonacci(i - 2);
    }

对于递归算法来说,代码一般都比较简短,从算法的逻辑上看,所用的存储空间也很小,但运行时的内存不一定会少

在讲解递归的时间复杂度时,我们提到了递归算法的时间复杂度本质上是递归的次数与每次递归的时间复杂度的乘积,可以看出,上面代码的每次递归都是时间复杂度为O(1)的操作,这里将以i为4的情况代入,可以抽象为一棵递归树:

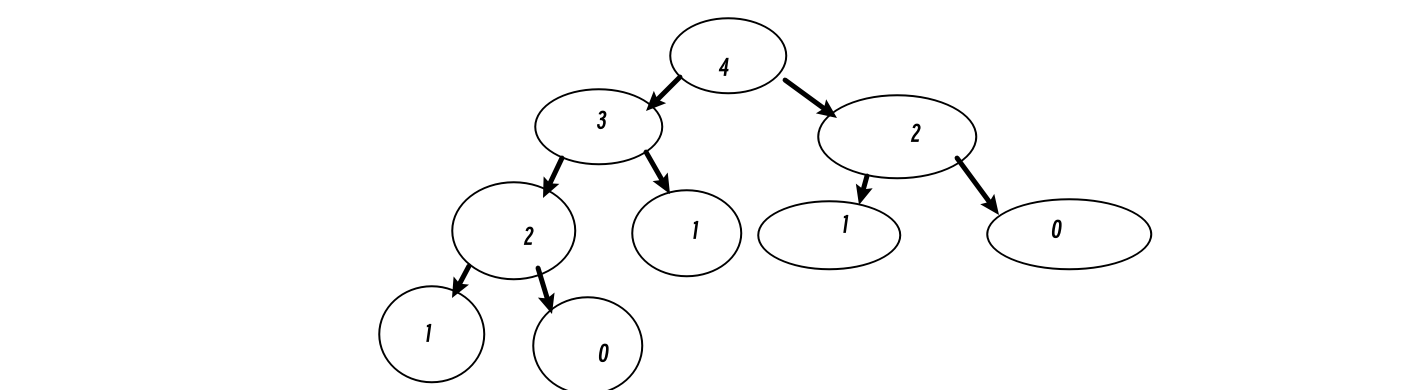
一颗深度(根节点的深度为1)为k的二叉树最多可以拥有2^k-1个节点,那么其时间复杂度为2ⁿ

这种指数级别的复杂度是非常大的,一般不推荐用这种方式求斐波那契数

如何求这段代码的空间复杂度呢?

公式:递归算法的空间复杂度=每次递归的时间复杂度*递归深度

为什么要求递归深度呢?

因为每次递归所需的空间都被压到调用栈里(这是内存管理的数据结构,和算法中的栈的原理是一样的),一次递归结束,这个栈就把本次递归的数据弹出去,所以这个栈的最大长度就是递归的深度

该代码因为每次递归的空间大小是一样的,所以每次递归所需的空间是一个常数,不会随着n的变化而变化,所以每次递归的空间复杂度为O(1)

递归深度由n控制,故递归深度为n

所以该代码的空间复杂度为O(n),时间复杂度为O(2ⁿ),非常耗时

罪魁祸首就是 “return fibonacci(i – 1) + fibonacci(i – 2);”这段代码大大啊增加了递归次数

优化:

int fibonacci(int first, int second, int n)
    {
      if(n<= 0)
            return 0;
        if(n <3)
            return 1;
        else if(n==3)
            return first + second;
        else
            return fibonacci(second, first + second, n - 1);
    }

因为每次递归的时候n-1,所以只递归了n次,所以时间复杂度为O(n)

递归的深度依旧是n,每次递归所需空间仍为常数,所以空间复杂度为O(n)

求斐波那契数	时间复杂度	空间复杂度
非递归算法	O(n)	O(1)
递归算法	O(2ⁿ)	O(n)
优化递归算法	O(n)	O(n)

可以看出,使用递归算法在性能上不一定是最优的,但递归算法确实让代码看上去更简洁一些

2.二分法的性能分析:

int binary_search(int arr[], int l, int r, int x)
    {
        if (r >= l)
            {
                int mid = l + (r - l) / 2;
                if (arr[mid] == x)
                    return mid;
                if (arr[mid] > x)
                    return binary_search(arr, l, mid - 1, x);
                return binary_search(arr, mid + 1, r, x);
            }
        return -1;
    }

二分查找的时间复杂度是O(logn),那么其空间复杂度是多少呢?

在c/c++中,递归函数传递的数组参数是首元素地址,而不是整个数组,也就是说,每一层递归都共用一块数组地址空间,所以每次递归的空间复杂度是O(1)

再来看递归的深度,二分查找的递归深度是logn,所以空间复杂度是O(logn)

要注意自己所用的语言在传递数组时,时复制的整个数组还是地址,如果复制的时数组,则空间复杂度为O(nlogn)

以空间换时间是常见的优化思路

即消耗更多内存以更快的计算出结果

在哈希法中,使用数组,set,map,等容器无一例外是基于以空间换时间的思路

发表评论 取消回复

发表评论取消回复